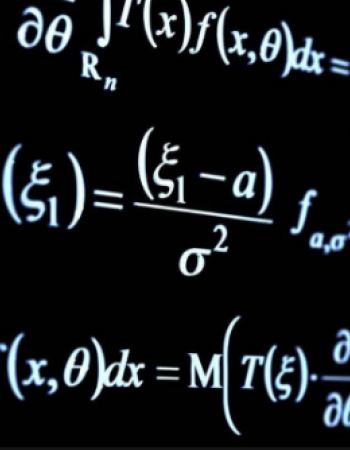Maximum principle for BSDEs with locally Lipschitz and logarithmic growth
This paper tackles a stochastic control problem involving a backward stochastic
differential equation (BSDE) with a local Lipschitz coefficient and logarithmic growth.
We derive the necessary and sufficient conditions for optimality that hold for all
optimal controls, even without convexity assumptions on the control domain. These
conditions involve a local Lipschitz stochastic differential equation and a minimized
Hamiltonian. We begin by demonstrating the existence and uniqueness of the
solution to the associated adjoint equation under suitable conditions. Next, we
introduce a series of control problems with global Lipschitz coefficients using an
approximation approach. This framework allows us to derive a stochastic maximum
principle, facilitating the analysis of near-optimal controls within these approximated
systems. Finally, we seamlessly transition back to the initial control problem through a
well-defined limit process.

We study both Malliavin regularity and numerical approximation schemes for a class of quadratic backward stochastic differential equations (QBSDEs for short) in cases where the terminal data need…

This paper tackles a stochastic control problem involving a backward stochastic
differential equation (BSDE) with a local Lipschitz coefficient and logarithmic growth.
We derive…