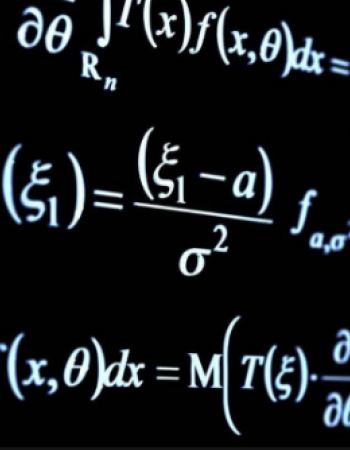Multidimensional Markovian BSDEs with Jumps and Continuous Generators
We deal with a multidimensional Markovian backward stochastic differential equation driven by a Poisson random measure and independent Brownian motion (BSDEJ for short). As a first result, we prove, under the Lipschitz condition, that the BSDEJs adapted solution can be represented in terms of a given Markov process and some deterministic functions
Then, by means of this representation, we show existence results for such equations assuming that their generators are totally or partially continuous with respect to their variables and satisfy the usual linear growth conditions. The ideas of the proofs are to approximate the generator by a suitable sequence of Lipschitz functions via convolutions with mollifiers and make use of the L2 domination condition, on the law of the underlying Markov process, for which several examples are given.

We deal with a multidimensional Markovian backward stochastic differential equation driven by a Poisson random measure and independent Brownian motion (BSDEJ for short).

We study both Malliavin regularity and numerical approximation schemes for a class of quadratic backward stochastic differential equations (QBSDEs for short) in cases where the terminal data need…

This paper tackles a stochastic control problem involving a backward stochastic
differential equation (BSDE) with a local Lipschitz coefficient and logarithmic growth.
We derive…